Receptor Terminology; Law of Mass Action

Brief Historical Background

Some terms and definitions

Affinity: the "tenacity" by which a drugs binds to its receptor.
Discussion: the solution of a lipid containing drug in the bilayer may be essentially irreversible: is this a high affinity event?
Intrinsic activity (=efficacy?): the relative maximal response caused by a drug in a tissue preparation. A full agonist causes a maximal effect equal to that of the endogenous ligand (or sometimes another reference compound if the endogenous ligand is not known); a partial agonist causes less than a maximal response.
Intrinsic efficacy: a drug’s ability to affect a receptor and cause a biological response (hence a property of a drug). (Discussion: can a drug have "negative efficacy"?).
Potency: broad definition: wide the ability of a drug to cause a measured biological change; narrow definition: wide the ability of a drug to cause a measured functional change.

The pharmacologist’s dream:

From a pharmacological perspective, one might simplify drug, hormone, or neurotransmitter action via the following scheme:

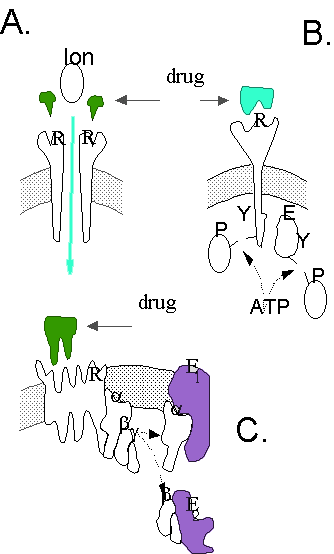
Ideally, we would wish to understand, and then predict, all of the properties of how a drug can cause a response in any tissue. Unfortunately, there are many factors that make achieving this goal at best difficult, and at worst, impossible. For example, events that affect the equilibrium of the drug at the receptor (limited diffusion on a macro or micro scale, metabolism, entrapment, etc.) can cause experimental results to deviate from theory. Even more importantly, the production of a stimulus often does not have a one-to-one correspondence to the measured response. The response caused by an activated receptor can involve a variety of different mechanisms (see cartoon in Figure 1). Some receptors directly effect the response of interest (e.g., the ionotropic receptor in A.). Even in this case, other factors (including allosteric modulators, cofactors, etc.) that can influence the observed response. In other cases, like a tyrosine kinase (B.), the receptor may itself be modified (e.g., phosphorylated) in the process of catalyzing a reaction (phosphorylation in this example). In the case of G protein coupled receptors (C.), the receptor may start a cascade of biochemical events due to actions at several effectors, and in some cases, also may be phosphorylated itself.

Theories of Drug-Receptor Interaction

There have been several major theories that have been proposed to provide a theoretical basis for understanding, modeling, and thereby predicting, drug response. Three of the most widely known of these schemes are described as follows:

Occupation Theory: the idea that a response emanates from a receptor only when it is occupied by an appropriate ligand (drug).
Rate Theory: the idea that a response emanates from a receptor in proportion to the kinetic rate of onset and offset of drug binding to the receptor.
Operational Model: a modified, semi-empirical approach that is based on occupancy theory modified to incorporate a factor relating agonist-receptor complex and response.

All of these theories have specific strengths and appeal, and all have significant failings. In general, rate theory is now considered to be the one of least utility. Conversely, since the advent of radioreceptor methods in the mid-1970’s, it is now possible to measure drug-receptor interactions directly, making occupation theory of particular interest because receptor occupation can be measured directly for the first time. As molecular tools begin to provide ways of studying several sequential molecular events, operational theory or direct multi-step models can certainly be applied.

Law of Mass Action

Although there are a plethora of complexities that arise, it is true that the large majority of experiments [especially those using radioreceptor methods (radioligand binding methods)] are based on very simple application of the law of mass action. In the case of a drug (ligand) interacting with a homogeneous population of receptors, this relationship can be expressed:

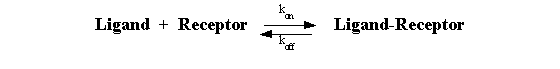
Binding occurs when ligand and receptor collide (due to diffusion) in the correct orientation and with enough energy. The rate of association (number of binding events per unit of time) equals [Ligand]*[Receptor]*k_on.

Once binding has occurred, the ligand and receptor remain bound together for a random amount of time. The rate of dissociation (number of dissociation events per unit time) equals [ligand*receptor]*k_off. The probability of dissociation is the same at every instant of time. The receptor doesn't "know" how long it has been bound to the ligand. After dissociation, the ligand and receptor are the same as at they were before binding. If either the ligand or receptor are chemically modified, then the binding does not follow the law of mass action.

Equilibrium is reached when the rate of formation of new ligand-receptor complexes equals the rate at which existing ligand*receptor complexes dissociate. By definition, at equilibrium this means that:

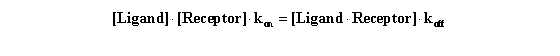
Rearrange that equation to define the equilibrium dissociation constant K_D.

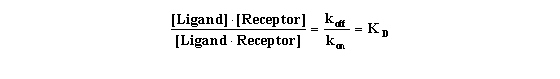
This equation gives you a feel for what K_D means. When the ligand occupies half the receptors, the concentration of unoccupied receptors equals the concentration of occupied receptors: [Receptor] = [Ligand*Receptor].This can only be true when K_D equals [Ligand]. In other words, the K_D is the concentration of ligand that, at equilibrium, will cause binding to half the receptors.

REMEMBER, the K_D is the equilibrium dissociation constant, whereas the k_off is the dissociation rate constant. The two measure different things and are expressed in different units.

Variable Name Units

kon Association rate constant or "on" rate constant M^-1min^-1

k_off Dissociation rate constant or "off" rate constant min^-1

K_D Equilibrium dissociation constant M

K_A Equilibrium association constant (=1/K_D) M^-1

A term that is sometimes useful to pharmacologists is fractional occupancy. Based on the law of mass action, this term describes receptor occupancy at equilibrium as a function of ligand concentration. Specifically:

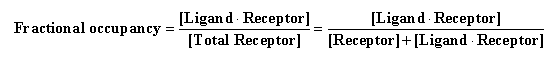
From the equation for K_D derived above, it is seen that:

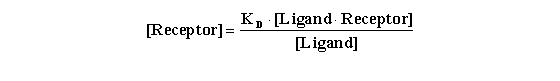
One can substitute this value for [Receptor] in the denominator of the equation for fractional occupancy and after simplifying, obtain the following (Do this yourself to see if it’s correct):

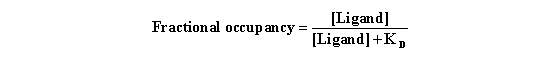
This equation assumes equilibrium. To make sense of it, think about a few different values for [Ligand]. When [Ligand]=0, the occupancy equals zero. When [Ligand] is very high (many times K_D) , the fractional occupancy approaches 100%. When [Ligand]=K_D, fractional occupancy is 50%.

Although termed a "law", the law of mass action is simply a model that can be used to explain some experimental data. As noted above, this model is not useful in all situations.

The model assumes that all receptors are equally accessible to ligands.
The model ignores any states of partial binding. According to the model, receptors are either free or bound to ligand. It also doesn’t allow for more than one affinity state (although this can be accommodated in some ways).
The model assumes that the ligand is not altered by binding.
The model assumes that binding is reversible.

Just because binding is constant over time does not mean the system is in equilibrium. Other reactions could be happening as well, especially when agonists are used. Many investigators use the term "steady state" to describe binding that has plateaued, and reserve the term "equilibrium" to describe the ideal model.

The Theoretical Basis for Characterizing Receptors using Saturation Radioligand Assays

Radioreceptor assays were first developed in the early 1970’s. They were based on two very simple, but very elegant concepts.

If a ligand had high affinity for a macromolecular target (as had been shown by classical pharmacological studies over many decades), it should be thermodynamically possible to measure the binding of the ligand to the receptor without the need to perform equilibrium dialysis (the only method then used) as long as one could separate the ligand-receptor complex from the free ligand.
By labeling ligands with appropriate radioactive atoms, one could detect the ligand-receptor sensitively and rapidly. (This was the key point, since chemical methods were neither sufficiently sensitive nor inexpensive for this use.)

The sections that follow will discuss many of the actual considerations for such assays, but it is first important to understand the conceptual basis for this approach. We begin with the simple law of mass action derived earlier:

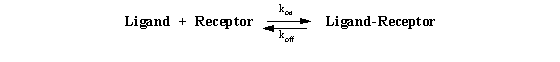
which led to the following equation:

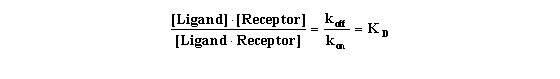
The receptor that has radioligand bound to it is called, in lab jargon, "Bound" or "B". The ligand that is not bound to receptor is called "Free" or "F". Both of these are measurable experimentally, as will be discussed below. This allows us to substitute these more common terms in the previous equation.

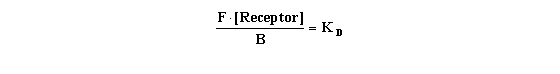
Since F and B are independent variables, and we wish to solve for K_D, it is necessary to be able to quantify the unbound receptor. This is technically impossible at present. Yet we know that:

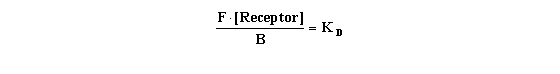
In fact, the total amount of receptor present (i.e., the maximal number of binding sites) is termed "B_max" in lab jargon, and is another desired experimental parameter. Thus, with more common lab terms:

or by rearranging:

If we take the equation from above:

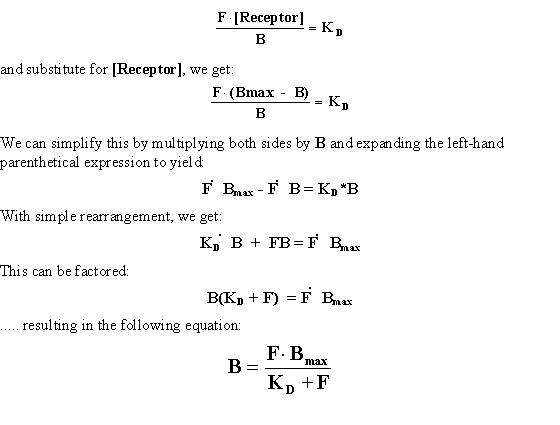
This equation should make clear the experimental design. One has an independent variable (F) and a dependent variable (B), and a successful experiment should allow one to arrive at estimates of two biologically meaningful constants: K_D and B_max. Hopefully this equation will look somewhat familiar, as it is functionally identical to the Michaelis-Menten equation of enzyme kinetics.