Antagonism
Antagonism is the process of inhibiting or preventing an agonist-induced
receptor response. Agents that produce this effect are called antagonists. The availability of selective antagonists
has provided an important mechanistic tool. On the one hand, the classification of receptor subtypes was accomplished largely
because of the availability of selective antagonists. Even with the proliferation of receptors resulting from molecular cloning,
selective antagonists are an essential element of understanding the functional role of such receptors. Based on the kinetics
of interaction of the antagonist with the receptor, antagonism is classified as competitive and non-competitive.
Competitive Antagonism.
Competitive antagonism is based on the principle that an agonist
or antagonist can bind to the same recognition site(s) on the receptor, and when both agonist and antagonist are present concomitantly,
they can compete for such sites. Reversible competitive antagonism occurs either when the binding of the antagonist can be
eliminated by increasing the concentration of agonist, or when the antagonist dissociates as the free concentration decreases.
The ability of an antagonist to influence the receptor occupancy
by an agonist (and therefore to elicit a response) is determined by the relative affinity of the antagonist for the receptor,
and by the relative concentration of the antagonist. Antagonism can be viewed as two independent equilibria occurring for
agonist (A) and antagonist (B):
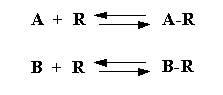
Based on the concentrations and equilibrium dissociation constants
of both agonist and antagonist, Gaddum derived the equation that predicts the effects of antagonists on the fraction of receptors
occupied by the agonist:
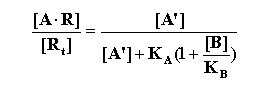
Where [A] is the concentration of agonist; [A'], the
concentration of agonist that in the presence of the antagonist, [B] is necessary to produce the same response as [A];
RT is the total receptor population, and KA and KB, the equilibrium
dissociation constants of the agonist and antagonist, respectively.
The effects of competitive antagonists on agonist induced responses
is studied by determining the dose-response relationships for the agonists in the absence or in the presence of increasing
concentrations of antagonists. This system assumes that the response of the test system depends only on the agonist occupancy,
and therefore, that equal agonist occupancies in the absence or in the presence of antagonist will produce equal responses.
The multiple increase in the agonist concentration required to achieve a given response is called the dose ratio. This
can be seen in the following Figure.
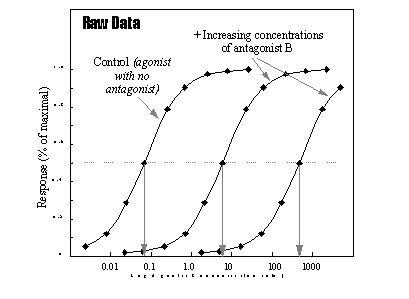
Log Agonist Concentration (nM)
The effects of two concentrations of antagonist on agonist
response.
Schild simplified Gaddum’s equation to the following:
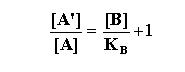
As you can see this formulation permits the assessment of KB
without making assumptions regarding the relationship between fractional occupancy and the ultimate response.
An empirical scale for antagonist potencies based on dose ratios
termed the pAX scale was introduced by Schild in 1949.
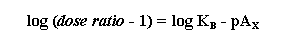
pAX is defined as the negative logarithm of the molar
concentration of antagonist that produces an equiactive dose ratio of magnitude x. For example, the pA10 is the
concentration of antagonist that produces a 10-fold shift to the right in the agonist dose response curve. Notice that the
pAX is an empirical value with no theoretical relevance to molecular mechanisms.
Schild Regression
The dose ratios calculated for a competitive antagonist can be used
in a quantitative model of competitive antagonism derived by Arunlakshana and Schild.
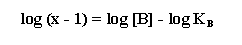

For clarity, this figure shows the effects of two concentration
of antagonist on agonist response. This analysis requires a minimum of five concentrations for an accurate analysis. The figure
above shows the fractional receptor occupancies by the agonist in the absence and in the presence of various concentrations
of antagonist. The receptor occupancy curve is shifted to the right in the presence of antagonist.

Notice that the dose ratio is referred to as x in the Schild
regression.
This equation is a powerful tool in the drug and receptor classification
process. If a regression of log (x-1) vs. log [B] is linear and has a slope of unity, it indicates that the
antagonism is competitive. This relationship is independent of the characteristics of the agonist, and should be the same
for all agonists that act on the same population of receptors.
Notice that the dose ratio depends only on the concentration
and on the equilibrium dissociation constant of the antagonist. The dose ratio is independent of the magnitude of the
response chosen as a reference point for the measurements and of the equilibrium dissociation constant of the agonist.
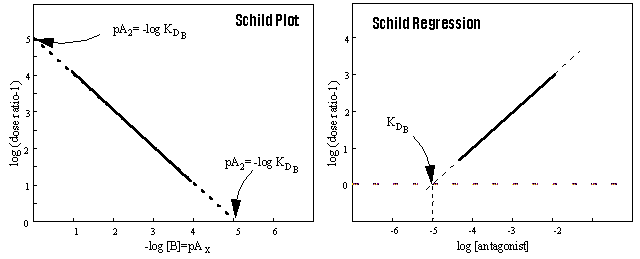
The intercept on the x axis of a plot of log (x -1) versus
log [B] yields directly KB, the equilibrium dissociation constant for the antagonist. The term pKB
is the value of -log (x-1) when the dose ratio (x) = 2. This quantity therefore corresponds to pA2, the
empirical parameter defined as the negative logarithm of the molar concentration of the antagonist that produce a dose ratio
= 2. Therefore, the pKB always correspond to the pA2. The opposite is only true, however,
when the Schild regression has a slope of unity.
An important practical aspect of experimental Schild regressions
is that sufficient equilibration time should be allowed to achieve a thermodynamic equilibrium between the antagonist and
the receptor before the challenge with the agonist.
Schild regressions with slopes different from unity can be originated
by:
- The antagonist is non competitive. i.e. interacts with the receptor
at non overlapping sites with agonist binding sites.
- A drug disposition mechanism or other nonequilibrium steady state
obscures the competitive nature of the antagonism
- The competitive antagonism of a heterogeneous receptor population
subserving the same response is observed; or
- Multiple drug properties are expressed in the concentrations used
to make the measurements (such as effects on agonist degradation or uptake).
Noncompetitive Antagonism.
In this type of antagonism, the blockade of agonist response is
produced by the interaction of the antagonist with binding sites intimately associated with the receptor, but distinct from
the agonist binding site. It is assumed that the binding of the antagonist to this site precludes the activation of the receptor
by the agonist. This could be conceptualized as if the noncompetitive antagonist removes the receptor, or eliminates the system's
capacity to respond. Therefore, the maximal capacity of the receptor to respond is decreased due to a progressive decline
in agonist fractional receptor occupancy. The agonist, however, operates normally at receptor-effector units not influenced
by the antagonist. The affinity of the remaining receptors for the agonist, and the potency of the agonist are not altered.
This type of antagonism is not surmountable by increasing the concentration of agonist.

Note:

|
In a situation where "spare receptors" are present,
the presence of a noncompetitive antagonist will first shift to the right the dose response of the agonist without a change
in the maximal response (pseudo competitive antagonism). Increasing the concentration of the non competitive antagonist will
eventually reduce the number of available receptors so that the maximal response can not be obtained.
|
