Competitive Binding Data with One Class of Receptors

Present and future uses of competition binding assays

It is too expensive and too technically challenging to characterize receptors only by direct radioligand binding assays. Moreover, when studying a new drug, it is usually not feasible to radiolabel the drug prior to understanding its receptor properties. For these reasons, competition assays are used most widely in receptor studies. One of the interesting new approaches in drug design and development is an elegant brute force approach called combinatorial chemistry. In this approach, one starts with several structural backbones that are felt likely to be components of a receptor pharmacophore (the structural features of a drug that cause binding and/or activation or blockade) and does chemical reactions that allow several different "pieces" to react in a way that hundreds of products may be formed. Rather than separating this gemisch and testing each component, the mixture is tested, and if the mixture is found to be "positive", the active species are purified and studied more conventionally. Such an approach dramatically increases the throughput of tested compounds. The most commonly used test system in combinatorial chemistry is the radioreceptor assay!

What is a competitive binding curve?

Competitive binding experiments measure the binding of a single concentration of labeled ligand in the presence of various concentrations of unlabeled ligand. Typically, the concentration of unlabeled ligand varies over at least six orders of magnitude.

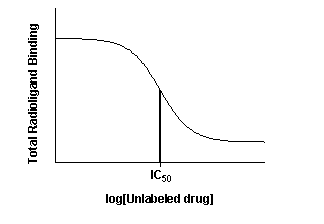
The top of the curve is a plateau at a value equal to radioligand binding in the absence of the competing unlabeled drug. The bottom of the curve is a plateau equal to nonspecific binding. The concentration of unlabeled drug that produces radioligand binding half way between the upper and lower plateaus is called the IC50 (inhibitory concentration 50%) or EC50 (effective concentration 50%).

If the radioligand and competitor both bind reversibly to a single binding site, binding at equilibrium follows this equation (where Top and Bottom are the Y values at the top and bottom plateau of the curve).

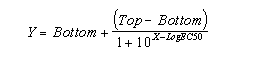
Competitive binding experiments are often used in more complicated situations where this equation doesn't apply.

Entering data

If you performed an experiment with triplicate samples and you are using software for analysis, let the software automatically plot the error bars. Some investigators transform their data to percent specific binding. The problem with this approach is that you need to define how many cpm equal 100% binding and how many equal 0% specific binding. Deciding on these values is usually somewhat arbitrary. It is usually better to enter the data as cpm.

Decisions to make before fitting the data

Weighting

When analyzing the data, you need to decide whether to minimize the sum of the square of the absolute distances of the points from the curve or to minimize the sum of the square of the relative distances. The choice depends on the source of the experimental error. Follow these guidelines:

If the bulk of the error comes from pipetting, the standard deviation of replicate measurements will be, on average, a constant fraction of the amount of binding. In a typical experiment, for example, the highest amount of binding might be 2000 cpm with a SD of 100 cpm. The low-est binding might be 400 cpm with a SD of 20 cpm. With data like this, you should evaluate goodness-of-fit with relative distances. The details on how to do this are in the next section.
You should only consider weighting by relative distances when you are analyzing total binding data. When analyzing specific binding (or data normalized to percent inhibi-tion), you should evaluate goodness-of-fit using absolute distances, as there is no clear relationship between the amount of scatter and the amount of specific binding.

Constants

With experience, you will notice that even with the use of the best software, data that is non-ideal (i.e., most data) requires the experimenter to make decisions during the course of the analysis. Many times, your data will span a wide range of concentrations of unlabeled drug, and clearly define the bottom or top plateaus of the curve. If this is the case, software can estimate with accuracy the 0% and 100% values from the plateaus of the curve.

In some cases, your competition data may not define a clear bottom plateau, but you can define the plateau from other data. All drugs that bind to the same receptor should compete all specific radioligand binding and reach the same bottom plateau value. This means that you can define the 0% value (the bottom plateau of the curve) by measuring radioligand binding in the presence of a standard drug at a concentration known to block all specific binding. If you do this, make sure that you use plenty of replicates to determine this value accurately. If your definition of the lower plateau is wrong, the values for the EC50 will be wrong as well. You can also define the top plateau as binding in the absence of any competitor.

To summarize, if you have collected enough data to clearly define the entire curve, let the software fit all the variables and fit the top and bottom plateaus based on the overall shape of your data. If your data do not define a clear top or bottom plateau, you should define one or both of these values to be constants fixed to values determined from other data. Because of factors such as intra-assay drift, this often provides a challenge to the investigator. In the class exercises, change the top and bottom values, and observe the effects on the derived variables and the fitted curve.

Interpreting the results

Assumptions

To interpret the results, you must make these assumptions:

Only a small fraction of your radiolabeled ligand binds to the tissue so that the free concentration is virtually the same as the added concentration. (There are alternative methods that do not make this assumption.)
There is no cooperativity.
Your experiment has reached equilibrium.
Binding is reversible and follows the law of mass action.
You use a valid value for the K_D of the radioligand (e.g., under similar conditions with a similar receptor).

IC50

The IC50 is influenced by three theoretical factors (in addition to the factors controlled, or affected, by the experimenter :

The affinity of the receptor for the competing drug (as reflected by its theoretical K_D). If the affinity is high (i.e., small K_D) the IC50 will be low.
The concentration of the radioligand. If you choose to use a higher concentration of radioligand, it will take a larger concentration of unlabeled drug to compete for the binding.
The affinity of the radioligand for the receptor (K_D). It takes more unlabeled drug to compete for a tightly bound radioligand (small K_D) than for a loosely bound radioligand (high K_D).

K_I

The K_I is an equilibrium dissociation constant. It is the concentration of the competing ligand that would bind to half the binding sites at equilibrium in the absence of radioligand or other competitors.
The subscript "I" is used to indicate that the competitor inhibited radioligand binding. Thus, it is determined indirectly by measuring competition with a known radioligand.
The K_ican be calculated once the IC50 is determined, and the competition curve has been analyzed. Commonly, we use one of the equations from Cheng and Prusoff (Biochem. Pharmacol. 22: 3099-3108, 1973). Note that there is not one Cheng-Prusoff relationship, but several. The one below is for pure competition at a single site:

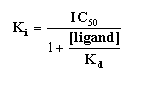
Shallow competitive binding curves

The slope factor or Hill slope

If the labeled and unlabeled ligand compete for a single binding site, the competitive binding curve will have a shape determined by the law of mass action. In this case, the curve will descend from 90% specific binding to 10% specific binding over an 81-fold increase in the concentration of the unlabeled drug. More simply, virtually the entire curve will cover two log units (100-fold change in concentration).

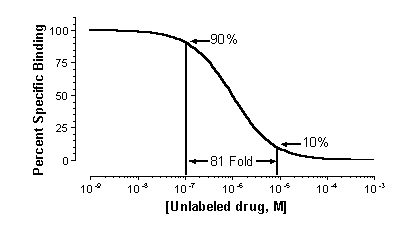
To quantify the steepness of a competitive binding curve, one determines a slope factor (also called Hill slope). A standard competitive binding curve that follows the law of mass action has a slope of -1.0. If the slope is more shallow, the slope factor will be a negative fraction (i.e. -0.85 or -0.60).

The Hill Equation

The Hill Equation provides information about the nature of ligand-receptor interactions. Widely used in the past, and often demanded by reviewers, its utility has been decreased by the wide availability of nonlinear regression analysis programs (like Prism, a program designed for receptor analysis). Thus, while less useful, it is important to understand the Hill equation since it has been a standard way of describing the slope factor (also called Hill slope or Hill number). It is derived from the binding equation modified to include the situation whereby the ligand may have multiple sites for interaction "n".

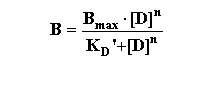
This can then be rearranged in several steps as follows:

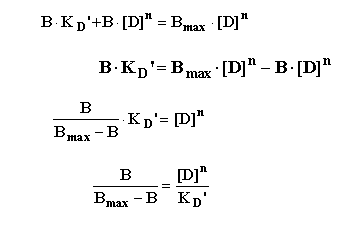
To yield the "Hill Equation".

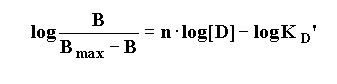
Thus, a plot of the log [Drug] vs. the logit function on the left hand side of the equation results in a straight-line with a slope = n_H. (the Hill slope or Hill number)

The slope factor describes the steepness of a curve. In most situations, there is no way to interpret the value in terms of chemistry or biology. If the slope factor is far from 1.0, then the binding does not follow the law of mass action with a single site. Often investigators transform the data to create a linear Hill plot. The slope of this plot equals the slope factor, and the intercept with an ordinate value of "0" equals the IC50.

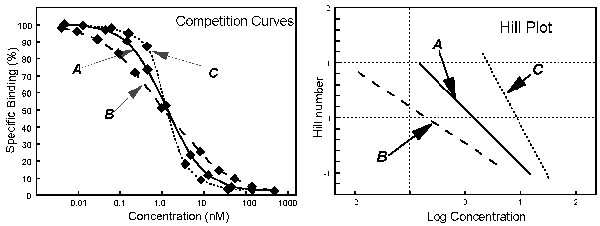
In these figures, A is a curve of normal steepness, with a Hill slope of 1. B is a curve of shallow steepness, with a Hill slope 1. C is a steep curve with a Hill slope 1

Explanations for shallow binding curves include:

Experimental problems. If the serial dilution of the unlabeled drug concentrations was done incorrectly, the slope factor is not meaningful.
Curve fitting problems. If the top and bottom plateaus are not correct, then the slope factor is not meaningful. Don't try to interpret the slope factor unless the curve has clear top and bottom plateaus.
Negative cooperativity. You will observe a shallow binding curve if the binding sites are clustered (perhaps several binding sites per molecule) and binding of the unlabeled ligand to one site causes the remaining site(s) to bind the unlabeled ligand with lower affinity.
Heterogeneous receptors. The receptors do not all bind the unlabeled drug with the same affinity.
Ternary complex model with limiting availability of G protein. This is a common situation that results with heterogeneous receptors. See below.

Competitive binding with two sites

Often, data does not fit one site models well, and a two site analysis may be useful. (Normal experimental variance usually does not permit discrimination of two from three high affinity sites). Some assumptions needed to do such analyses include:

There are two distinct classes of receptors. For example, a tissue could contain a mixture of b1 and b2 adrenergic receptors.
The unlabeled ligand has distinct affinities for the two sites.
The labeled ligand has equal affinity for both sites.
Binding has reached equilibrium.
A small fraction of both labeled and unlabeled ligand bind. This means that the concentration of labeled ligand added is very close to the free concentration in all tubes.

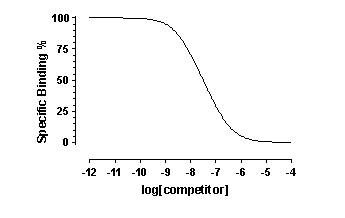
When you look at the competitive binding curve, you will only see a biphasic curve only in the rare cases where the affinities are very different. More often you will see a shallow curve with the two components blurred together. For example, this graph shows competition for two equally abundant sites with a ten fold (one log unit) difference in EC50. If you look carefully, you can see that the curve is shallow (it takes more than two log units to go from 90% to 10% competition), but you cannot see two distinct components.

Comparing one- and two-site models

Some software (like Prism) can simultaneously fit your data to two equations and compare the two fits. This feature is commonly used to compare a one-site competitive binding model and a two-site competitive binding model. Since the model has an extra parameter and thus the curve has an extra inflection point, the two-site model almost always fits the data better than the one site model. And a three site model would fit even better. Before accepting the more complicated models, you need to ask whether the improvement in goodness of fit is more than you would expect by chance. Prism, for example, answers this question with an F test that yields a P value that answers this question: If the one site model were really correct, what is the chance that randomly chosen data points would fit to a two-site model this much better (or more so) than to a one-site model?

Before looking at Prism’s comparison of the two equations, you should look at both fits yourself. Sometimes the two-site fit gives results that are clearly nonsense. Here are some examples to when to disregard a two-site fit:

The two IC50 values are almost identical.
One of the IC50 values is outside the range of your data.
The fraction of the total binding represented by any of the sites is either close to 1.0, or to 0.0. In this case, most of the receptors have the same affinity, and the IC50 value for the low occurring site cannot be reliable.
The calculated values for either the BOTTOM or TOP of your curves are far from the range of real values in your experiment.

Basic Principle: If the results don’t make sense, don’t believe them (don’t ever say "The computer said ...."). Only pay attention to the results of the comparison when both fits are reasonable.

This equation has five variables: the top and bottom plateau binding, the fraction of the receptors of the first class, and the IC50 of competition of the unlabeled ligand for both classes of receptors. If you know the K_D of the labeled ligand and its concentration, you can convert the IC50 values to K_ivalues.

Agonist binding and the ternary complex

If you use an antagonist radioligand and compete with an unlabeled agonist you are likely to observe a shallow competitive binding curve. Receptors can interact with intracellular molecules in a way that alters agonist binding. One situation that has been well studied is the competition of unlabeled agonist ligand for antagonist radioligands for binding to receptors linked to G proteins in membrane preparations lacking GTP.

The ternary complex model explains some of these data. This model shows binding of an agonist (A) to receptor (R) coupled to G protein (G):

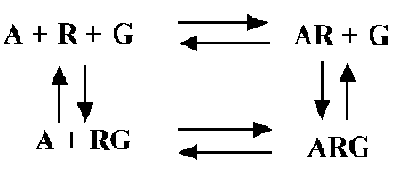
Some features of the model:

The left half of the picture shows the equilibrium between receptor (R) and G protein (G) in the absence of agonist (A).
The right half shows the agonist-receptor complex binding to G to form the ternary complex (ARG).
The top part shows the binding of agonist to receptors not linked to G.
The bottom part shows the binding of agonist to receptors linked to G.
Not shown is the radioligand L that binds with equal affinity to R and RG.
This model can explain the shape of agonist competition curves if the following are true:
- Agonist binds more tightly to the receptor-G complex than to receptor alone. In other words, A binds with low affinity to R but to high affinity to RG.
- The total concentration of G is limiting. If G is present in higher concentrations than R, this model does not predict shallow binding curves (Neubig et al. Mol. Pharmacol. 28:475, 1985).
- GTP is omitted from the incubation. When GTP is present, as it is inside cells, the model is more complicated. Soon after the ARG complex forms, GTP binds to the G protein, and activates it. The activated G then dissociates from AR, and its * subunit dissociates from the ** subunits. Because the ARG complex is so transient, all you see in binding experiments is low affinity AR binding.

A few investigators have fit data to equations describing the ternary complex. Most do not, for these reasons:

The model is too complicated to fit well. There are too many parameters to fit. You need to fit all four equilibrium constants, plus the relative concentration of receptor to G.
The model is too simple to be useful. The ternary complex model only predicts a shallow competitive binding curve when the total concentration of G is less than or equal to the total concentration of receptors. But biochemical evidence in many systems demonstrates that G is present in vastly higher concentrations than receptors. Yet these systems demonstrate shallow competitive binding curves. To resolve this discrepancy, you must make the model still more complicated (either many of the G proteins are not available to bind to receptors, or many of the receptors are not available to bind to G proteins). For a review of these issues, see RR Neubig, Faseb J. 8:939-946, 1994.

Rather than fit data to the ternary complex model, most investigators fit data to a two-site binding model. The data fit well to the two site model, even though we know it is too simple. The two-site model is shown below - it is not the same as the ternary complex model.

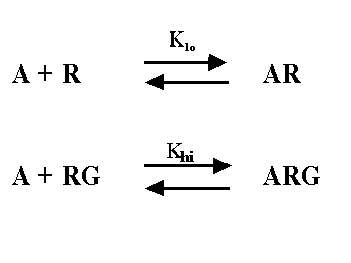
The two-site model, as its name implies, assumes that there are two distinct kinds of receptors. In this context, one kind of receptor is coupled to G, and the other is not. This simpler model provides values for K_lo, K_hi, and relative numbers of the two kinds of receptors, and these can be compared after different treatments. Since we know that the two-site model is too simple (the ternary complex is a better model for many systems) you shouldn't interpret K_hi and K_lostrictly. Nonetheless, the ratio of the K_hiand K_lois a useful empirical measure which often correlates with agonist efficacy.

This short section is hardly adequate to explain the complexities of the ternary complex model, but should be sufficient to keep you from making common mistakes in interpretation.

Ligand, Prism and other curve fitting programs

The first widely used program in the field was "Ligand", a freely available, special-purpose nonlinear regression program for analyzing equilibrium radioligand binding data written by Munson, Rodbard, and collaborators (Methods in Enzymology 92:543, 1983). Today, there are many other alternatives to Ligand (for many different computer platforms) that may be easier to use or more facile with certain types of analyses.